红黑树
红黑树的应用场景
# c++ stl map,set(红黑树的封装)
# 进程调度cfs(用红黑树存储进程的集合,把调度的时间作为key,那么树的左下角时间就是最小的)
# 内存管理(每次使用malloc的时候都会分配一块小内存出来,那么这么块就是用红黑树来存,如何表述一段内存块呢,用开始地址+长度来表示,所以key->开始地址,val->大小)
# epoll中使用红黑树管理socketfd
# nginx中使用红黑树管理定时器,中序遍历第一个就是最小的定时器红黑树的定义
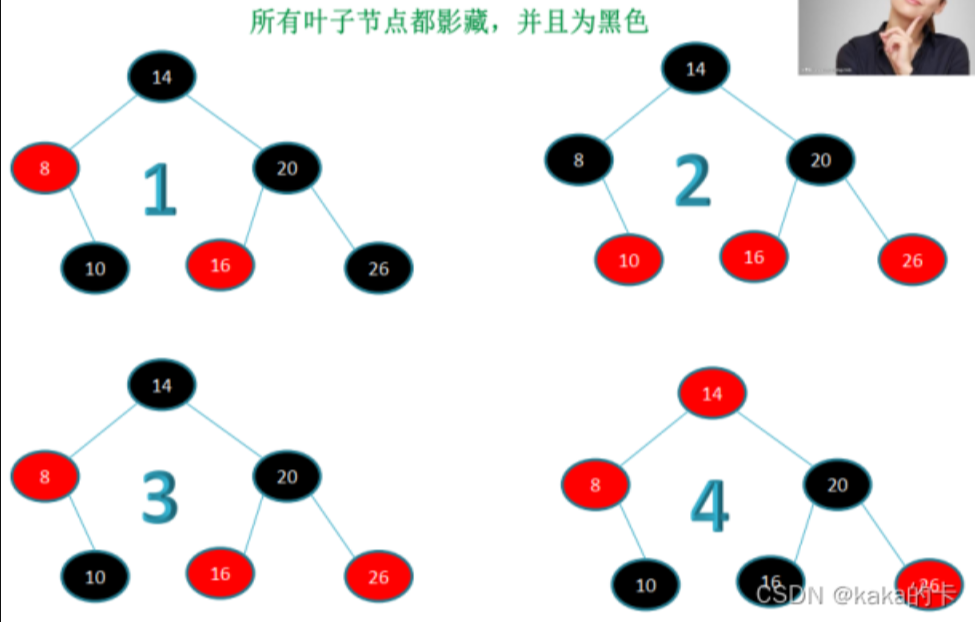
1. 每个结点是红的或者黑的
2. 根结点是黑的
3. 每个叶子结点是黑的(因为这条性质,一般用叶子结点在代码中被特殊表示)
4. 如果一个结点是红的,则它的两个儿子都是黑的(不存在相邻红色)
5. 从任一节点到叶子节点,所包含的黑色节点数目相同(即黑高度相同)
6. 最长路径长度不超过最短路径长度的2倍(2n-1,一条黑红黑红…一条全黑)2号是红黑树
红黑树结构体
typedef int KEY_TYPE;
//红黑树定义
typedef struct _rbtree_node {
unsigned char color; //颜色
struct rbtree_node *parent; //颜色
struct rbtree_node *left; //左子树
struct rbtree_node *right; //右子树
KEY_TYPE key;
void *value;
} rbtree_node; //红黑树结点
struct rbtree {
rbtree_node *root; //根结点
rbtree_node *nil; //通用叶子结点
}; //红黑树红黑树的旋转
红黑树性质被破坏的时候,调整。
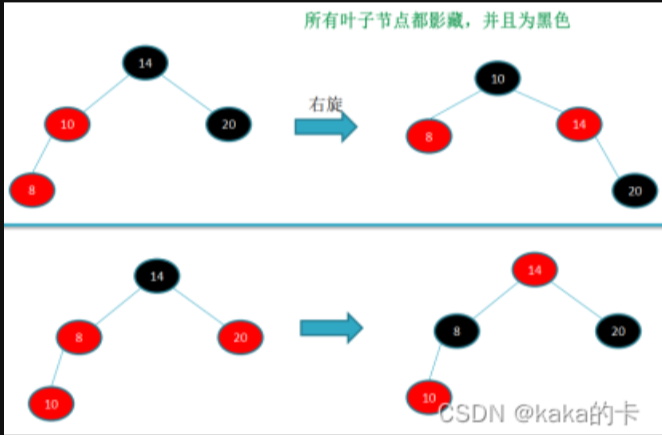
动三个方向,改6个指针。 通过旋转,调整左右高度,使树达到平衡。
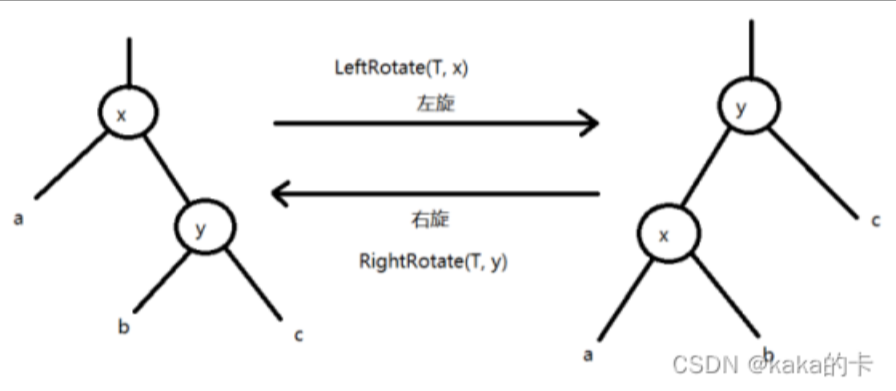
左旋 降低X结点的高度,提高X结点右结点(即Y)的高度。
x的右子树指向y的左子树
本来指向x结点的父指针,改成指向y
y的左子树指向x结点
1. //左旋 //降低X结点的高度,提高X结点右结点(即Y)的高度。 void rbtree_left_rotate(rbtree *T, rbtree_node *x) { if (x == T->nil) return ; rbtree_node *y = x->right; //1 x->right = y->left; //x的右子树指向y的左子树 if (y->left != T->nil) { y->left->parent = x; //y的左子树的父节点指向x } //2 y->parent = x->parent; //y的父结点指向x的父结点 if (x->parent == T->nil) { //如果x是根结点 T->root = y; } else if (x == x->parent->left) { x->parent->left = y; //x和父节点的左子树 } else { x->parent->right = y; //x和父节点的右子树 } //3 y->left = x; //y的左子树指向x结点 x->parent = y; //x的父节点指向y }
右旋 降低Y结点的高度,提高Y结点左结点(即X)的高度。
y的左子树指向x的右子树
本来指向y结点的父指针,改成指向x
x的右子树指向y结点
//右旋 //降低Y结点的高度,提高Y结点左结点(即X)的高度。 void _right_rotate(rbtree *T, rbtree_node *y) { rbtree_node *x = y->left; //1 y->left = x->right; //y的左子树指向y的右子树 if (x->right != T->nil) { x->right->parent = y; //x的右子树的父节点指向y } //2 x->parent = y->parent; //x的父结点指向y的父结点 if (y->parent == T->nil) { //如果y是根结点 T->root = x; } else if (y == y->parent->right) { y->parent->right = x; //y和父节点的右子树 } else { y->parent->left = x; //y和父节点的左子树 } //3 x->right = y; //x的左子树指向y结点 y->parent = x; //y的父节点指向y }
红黑树的插入
插入结点的颜色
在插入结点时,我们始终认为“插入这个结点之前,原来的红黑树是满足红黑树性质的==”,那么插入的位置容易找,就是不断的对比key,最终找到位置,那么新增的结点是什么颜色呢?
我们通过性质发现:
如果新结点是黑色,违背了第5条性质
如果新结点是红色,可能违背第4条性质
而第四条性质,我们可以通过旋转与上色的方式修复,所以在我们插入结点的时候,我们始终认为新结点是红色void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil; //初始化为空
rbtree_node *x = T->root; //根节点
while (x != T->nil) { //x不等于叶子结点
y = x; //y始终指向x前一个位置
if (z->key < x->key) {
x = x->left; //小于插左子树
} else if (z->key > x->key) {
x = x->right; //大于插左子树
} else { //Exist //等于
//如果key相等,看自己的业务情景
//重复插入可以不修改直接退出,可以修改val
}
}
z->parent = y;
if (y == T->nil) { //如果红黑树为空
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
//插入的结点
z->color = RED;
z->left = T->nil; //左右子树为空
z->right = T->nil;
//维护红黑树
rbtree_insert_fixup(T, z); //修复第4条性质
}通过旋转与上色的方式修复第4条性质 性质四:如果一个结点是红的,则它的两个儿子都是黑的(不存在相邻红色)
我们知道新增结点是红色,如果新结点是父节点也是红色,那么就需要维护红黑树了。
父结点是祖父结点是左子树的情况 在下面的图中:z表示新增结点,y表示叔结点
叔结点是红色的
将叔结点和父结点变黑,爷结点变红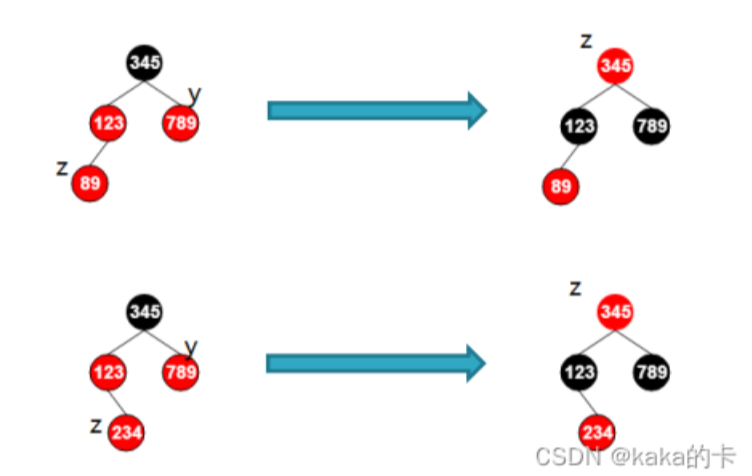
叔结点是黑色的,而且当前结点是右孩子
以父结点为中心左旋
将父结点变黑色,爷结点变红色
以爷结点为中心右旋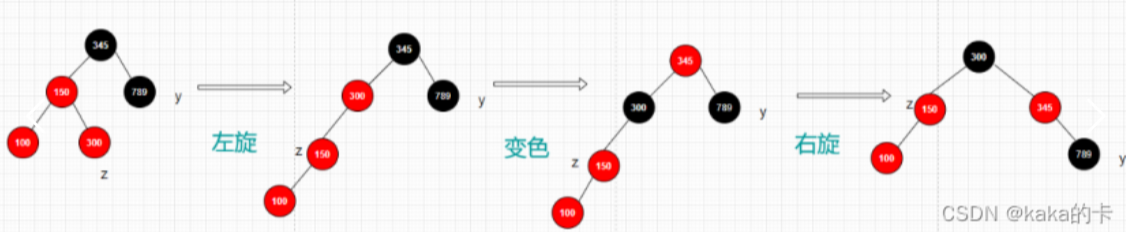
叔结点是黑色的,而且当前结点是左孩子
将父结点变成黑色,爷结点变成红色
以爷结点为中心右旋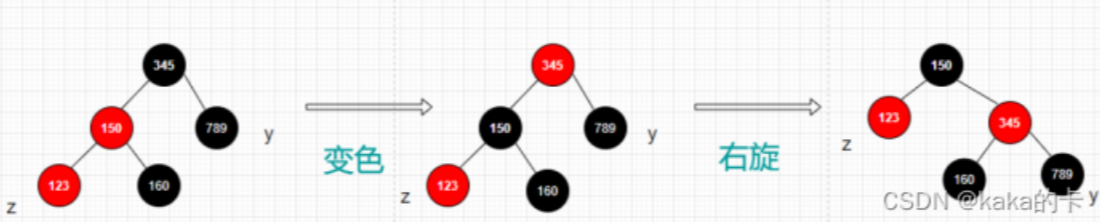
父结点是祖父结点是右子树的情况 修复的代码
//修复第4条性质
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
while (z->parent->color == RED) { //父结点是红色的,需要调整
if (z->parent == z->parent->parent->left) { //如果父结点是爷结点是左子树
rbtree_node *y = z->parent->parent->right; //叔结点
if (y->color == RED) { //叔结点是红色的
//先变色,叔,父变黑
z->parent->color = BLACK;
y->color = BLACK;
//爷结点变红
z->parent->parent->color = RED;
z = z->parent->parent; //递归
}
else {//叔父结点是黑色
if (z == z->parent->right) { //新节点是在右边
z = z->parent;
rbtree_left_rotate(T, z); //以父结点为中心左旋
}
//将父结点变成黑色,爷结点变成红色
z->parent->color = BLACK;
z->parent->parent->color = RED;
//以爷结点为中心右旋
rbtree_right_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK; //根节点始终是黑色
}红黑树删除
总结 红黑树的时间复杂度
rbTree查询元素:O(log(N))
rbTree插入元素:插入最多2次旋转,加上查询的时间O(log(N)),插入的复杂度O(log(N))
rbTree删除元素:删除最多需要3次旋转,加上查询的时间,删除的复杂度O(log(N))

